What is Sharpe Ratio? The term Sharpe ratio is actually not a complex or foreign language term in the financial world. This term has been used widely in the investment world. In the investment world, an investor would want to know the extent to which an investment can be said to be profitable, in terms of returns. The indicator can be measured by Sharpe ratio.
Sharpe ratio to measure Excess Returns
Sharpe ratio is a measure used to measure excess returns, or risk premiums, per unit deviation in investment assets or trading strategies. This measure is used to check investment performance by adjusting the risk. Sharpe ratio are also known by few other terms such as
- reward-to-variability ratio.
- Sharpe index,
- Sharpe measure
Calculation Formulas for Sharpe ratio
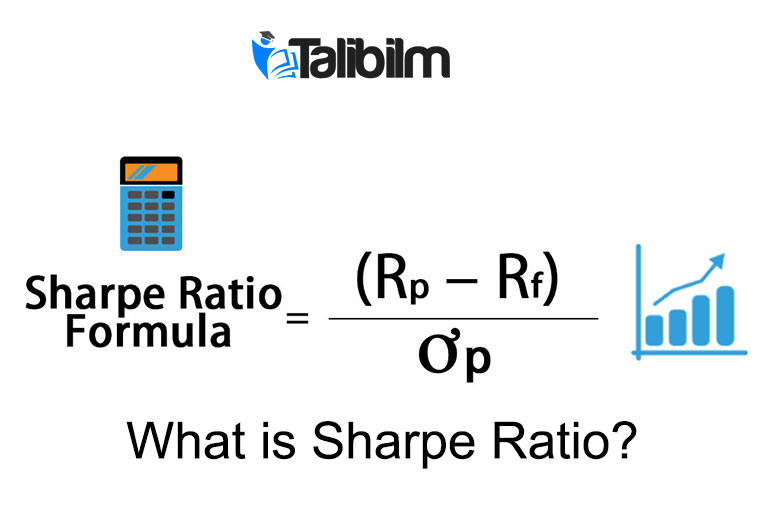
Sharpe ratio calculation is based on the calculation formula below:
Sharpe Ratio = (R p – R f ) / σ p
Investments with higher Sharpe ratio
The expected result to be obtained is that the value of the Sharpe ratio produces high values. The higher the value of the Sharpe ratio, the better the investment performance compared to the risk. In other words, if there are two types of investments with the same level of risk, then choose investments that have a higher Sharpe ratio value.
Negative Sharpe ratio
On the other hand, Sharpe ratio can also have negative values. A negative Sharpe ratio value indicates that the level of free risk is greater than the rate of return on the portfolio. Of course this is not desired by investors.
Meanwhile, if there are two investment portfolios that have the same return and free risk level, then a portfolio that has a high standard deviation or volatility will result in a lower Sharpe ratio value. Thus, the relationship between the value of Sharpe ratio with volatility is negative, which means that the higher the value of volatility, the lower the value of Sharpe ratio, and vice versa.
The use of Sharpe Ratio
Aside from being a measure of investment portfolio performance, the Sharpe ratio still has other uses. These uses include:
- Strengths and Weaknesses of Sharpe Ratio
- Sharpe ratio is the most widely used method for calculating the return on investment adjusted for risk.
- Sharpe ratio is useful for evaluating the performance of previous portfolios.
- Sharpe ratios would be considered whenever we want a comparison to compare changes in overall risk return results when new assets or asset classes are added to the portfolio.
Sharpe Ratio Indicators
In its development, sharpe ratio indicators have been statistically tested. Some researchers such as Jobson, Korkie, Gibblons, Ross & Shanken have conducted statistical research on Sharpe ratio indicators. Even so, Sharpe ratio indicators still have various strengths and weaknesses.
When calculating if the Sharpe ratio produces a negative value, that’s where the problem occurs. When ultimate value of Sharpe ratio is negative it is difficult to interpret. When other factors are considered constant, an investor will want to increase the rate of return on the portfolio and reduce the level of volatility.
Sharpe Ratio
In addition, the sharpe ratio indicator has an assumption that the return on assets has a normal distribution. Unfortunately, this assumption is in fact very difficult to fulfill. There are several problems that prevent the return of assets not to have a normal distribution. These problems are in the form of distribution curves which are actually problematic in kurtosis and skewness. Because the assumption of a normal distribution is difficult to fulfill, the effect is that the results of the calculation are not quite right.
Standard deviation formula in Sharpe Ratio
One other shortcoming contain in the Sharpe ratio is that it lies in one of the variables in the calculation formula. These variables are the standard deviation variables, or volatility. In essence, the standard deviation takes into account both positive and negative deviations from the average. Therefore, the standard deviation cannot accurately measure the risk of decline. As a result, the standard deviation is actually a very risky variable in the sharpe ratio calculation formula.